Cyclic Arbitrage in DEX 리뷰

Executive Summary

이 문서는 Cyclic Arbitrage in Decentralized Exchanges 논문을 읽고 BEARS 팀내 기술 세미나 자료로 활용하기 위해 작성되었으며, 이 논문을 분석한 목적은 DEX내에서 시세차익(Arbitrage)를 얻을 수 있는 방법에 대한 정보 수집을 목적으로 분석하였습니다.

Introduction

논문에서는 먼저 블록체인 생태계에서 Decentralized Finance(DeFi)의 비중이 증가(2021년 10월까지 1200억달러)하고 있음을 언급하면서 이 DeFi 환경의 핵심 서비스로 DEX를 언급하고 있습니다. 논문에서 중심으로 삼고 있는 DEX거래소는 Uniswap 거래소이며, 해당 거래소는 Constant Product Market Maker(CPMM) 거래소의 대표격(Coinmarket cap 시총 순위에서도 100위내 거래소)입니다. 그 전에 DEX 거래소는 Automatic Market Maker(AMM) 알고리즘의 기반으로 토큰간의 상대적 가치를 결정, 이를 통한 거래를 하게 되는데 기본적인 DeFi의 개념이 없다면 BEARS팀의 Grizzly가 작성한 내 마음대로 정리하는 DeFi 용어들를 한 번 읽어 보는 것을 추천합니다.

논문에서는 기존 삼각 시세차익(Triangular Arbitrage)를 염두하고, 접근 한 것으로 보입니다. 삼각 시세차익이라는 용어는 본 논문의 참고문헌을 기준으로 서로 다른 국가에 위치한 중앙화거래소(CEX)간 시간차를 활용한 시세차익을 의미하는 것으로 판단되며, 본 논문에서는 한 DEX 거래소내 3종류의 토큰 A, B. C가 존재할 때 $A \Leftrightarrow B$, $B \Leftrightarrow C$, $C \Leftrightarrow A$ 순서로 스왑핑(swapping) 거래가 이뤄 질 때 발생하는 시세차익을 삼각 시세차익으로 정의하고 있다고 봐도 될것 같습니다. CEX를 활용한 시세차익에서는 거래소가 삼각형의 꼭지점이 되는 것이고, 본 논문 DEX에서는 토큰이 꼭지점에 해당합니다.

Problem

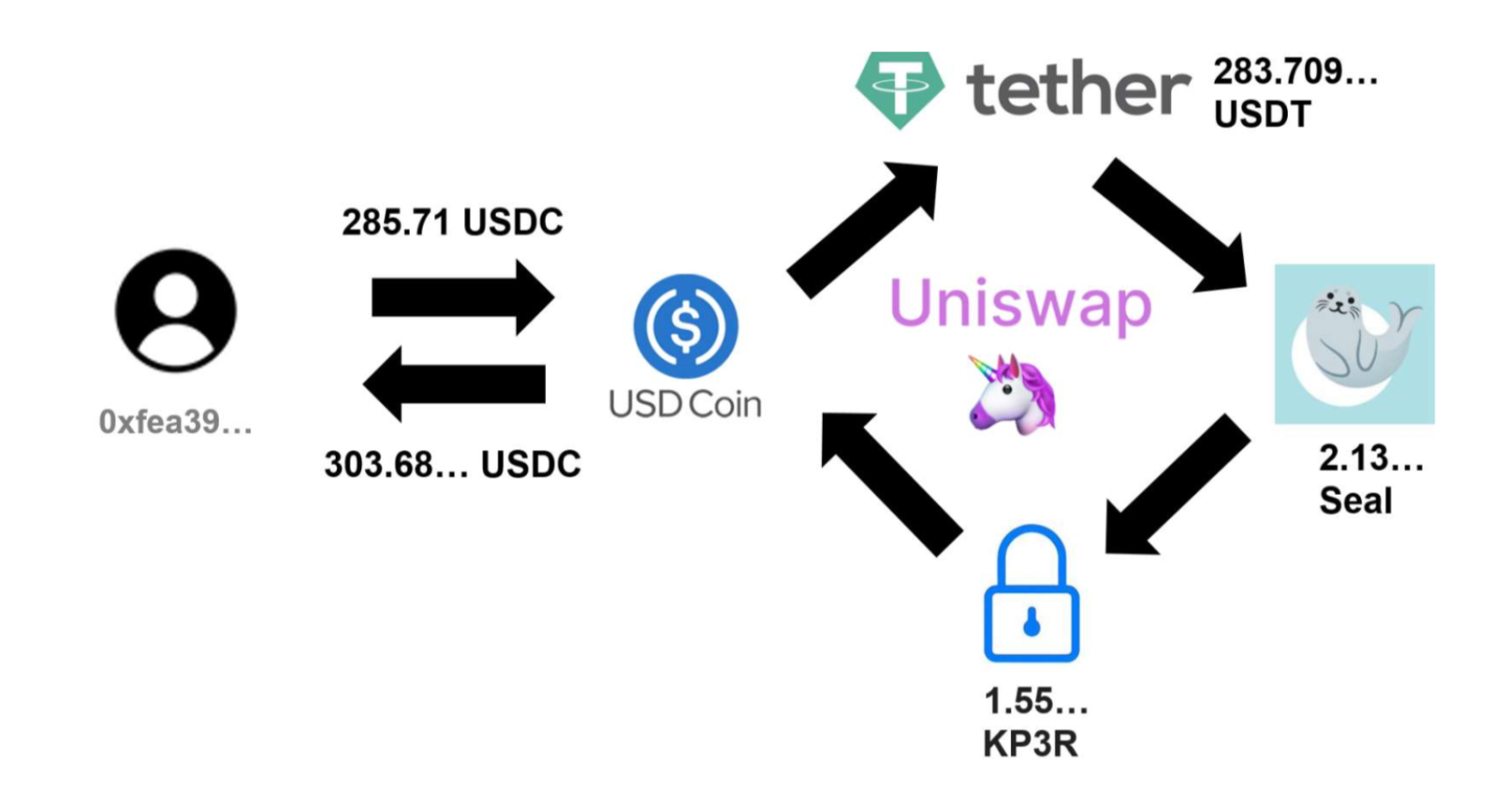
이 논문에서 해결하고자 한 문제는 한 DEX 거래서내에서 시세차익을 유발하는 거래를 시스템적으로 발견하는 방법론 및 그 때의 최적화된 토큰 거래량 결정 방법 도출이라고 할 수 있습니다. 이를 위해 Uniswap이라는 거래소를 목표로 설정하였고, 실제적으로 20년 5월4일부터 21년 4월15일까지의 Uniswap에서 발생하는 토큰 거래를 분석하였습니다. 아래 그림.1의 경우 논문에서 제시하고 있는 Uniswap에서 시세차익 거래를 표현한 것이며, 이는 꼭 Uniswap만 해당하는 것이 아닌, Constant Product Market Maker(CPMM) 알고리즘 방식의 모든 거래소에 해당합니다.

그림.1 Uniswap-V2에서의 시세차익의 예

Contribution

저자들이 얘기하는 본 논문의 기여부분은 다음과 같습니다.

• 암호자산 시장에서의 시세차익 거래 동작에 대해서 이론과 경험적 분석을 바탕으로한 첫번째 연구
• DEX 거래소내 순환 시세차익 거래에 대한 최신 평가방법 제공
• 블록체인 기술내에서 사용자들이 다양한 매매 전략을 사용하고 있음을 밝혀내고, DEX 거래소를 활용한 사용자들이 금융 거래에 대해서 이해도를 높임

Limitation

위에서 본 논문의 한계점은 연구범위라고 얘기할 수 있습니다. SoK: Decentralized Exchanges (DEX) with Automated Market Maker (AMM) Protocols 논문을 보면, DEX 거래소에서 사용하고 있는 Automatic Market Maker(AMM) 알고리즘 종류가 다양한 것을 확인할 수 있습니다. 그러나 본 논문에서는 CPMM 알고리즘 경우에만 적용할 수 있는 알고리즘을 제안하고 있어 해당 알고리즘을 적용할 수 있는 대상이 제한적입니다. 또한 분석 대상 거래소가 Uniswap뿐인 것도 조금 아쉽습니다. 현재 DEX 거래소는 1천여개가 넘어 간다고 알려져 있고, 이더리움 가스비 문제로 솔라나(Solana), 테라(Tera), 폴카닷(Polkadot)과 같은 체인에서도 DEX 거래소가 많이 생겨나고 있으며, 이 것을 ImmuneFi Bug Bounty 사이트에서도 확인할 수 있습니다. 그리고 Uniswap의 경우 swapping때의 CPMM의 문제를 보완하기 위해 Uniswap-V3를 출시한 상태이며 본 논문은 Uniswap-V2를 대상으로 하고 있는 점도 아쉽습니다. 따라서 Uniswap-V3에서 토큰 스왑핑(Swapping)만으로 해당 논문에서와 같이 시세차익이 유발할 수 있는지에 대해서는 추가적인 조사가 필요해 보입니다.

Background

CPMM(Constant Product Market Maker) : Uniswap V2

UniswapV2 swap function

CPMM의 스와핑때 기본 알고리즘은 $x \times y$ 를 일정하게 유지하는 것입니다. 만약 $X$ 토큰을 $\Delta x$ 만큼 팔고, 이후에 토큰 $Y$ 를 $\Delta y$ 만큼 구매하였다면, DEX 거래소 금고(Vault)관점에서는 아래과 같은 수식이 설립하여야 합니다. $ x \times y = (x + \Delta x) \times (y - \Delta y) $ 이 때의 $\Delta x$ , $\Delta y$ 는 아래와 같은 수식으로 유도 가능합니다.

\[x^{\prime} = x + \Delta x = (1 + \alpha)x = \frac{1}{1 - \beta}x\\ y^{\prime} = y - \Delta y = \frac{1}(1 + \alpha)y = {1 - \beta}y\]

이 때의 $\alpha = \frac{\Delta x}{x}$ 이고, $\beta = \frac{\Delta y}{y}$ 로 정의하면 우리가 구하고 싶은 토큰 변화량은 다음과 같다.

\[\Delta x = \frac{\beta}{1 - \beta}x\\ \Delta y = \frac{\alpha}{1 + \alpha}y\]

위 경우는 이상적인 경우의 수식이고 실제 스와핑 거래시 수수료가 존재합니다. 그럼 수수료는 $\rho$ 로 정의하면, $\rho$ 의 범위는 $0 \leq \rho <1$ 이 됩니다.

\[{x^{\prime}}_{\rho} = x + \Delta x = (1 + \alpha)x = \frac{1 + \beta(\frac{1}{\gamma} - 1)}{1 - \beta}x\\ {y^{\prime}}_{\rho} = y - \Delta y = \frac{1}{1 + \alpha \cdot \gamma}y = (1 - \beta)y\]

이 때의 $\alpha = \frac{\Delta x}{x}$ 이고, $\beta = \frac{\Delta y}{y}$ 이며, $\gamma = 1 - \rho$ 로 정의하면 우리가 구하고 싶은 토큰 변화량은 다음과 같습니다.

여기서 한 번 잘 생각해봐야 하는게 우리가 $\Delta x$ 만큼 토큰을 스와핑 하지만 여기에 수수료가 붙기 때문에 실제로 우리가 교환하게 되는 토큰은 $\Delta x \times \gamma$ 만큼이 됩니다. 엄밀히 말하면 $\Delta y$ 의 경우 $\Delta x \times \gamma$ 에 대응하는 변화량이 되는 것입니다.

이상적인 경우의 교환되는 $\Delta x$ 의 경우 아래의 수식이 성립하였으며

\[\Delta x = \frac{\beta}{1 - \beta}x\]

이를 수수료 모델에 대입하면, 아래의 수식이 성립하고

\[\gamma \cdot \Delta x = \frac{\beta}{1 - \beta} \cdot x\]

결국 $\Delta x$ 는 $\Delta x = {\frac{\beta}{1 - \beta}} \cdot {\frac{1}{\gamma}} \cdot x$

그럼 $\Delta y$ 를 구해보겠습니다. 이상적인 모델에서의 $\Delta y$ 와 구분하기 위해서 수수료가 적용된 모델에서의 $\Delta y$ 는 $\Delta y_{\rho}$ 로 하겠습니다. Formal Specification of Constant Product Market Maker Model and Implmemtation에서는 이 둘을 구분하지 않고 사용해서 처음에는 좀 혼돈이 있었습니다. 본 논문의 수수료 모델에서의 $\Delta y$ 는 이상적인 모델에서의 $\Delta y$ 의미가 동일한 것이 아닙니다.

이상적인 경우의 $\Delta y$는 아래와 같은 수식으로 표현하였습니다. \(\Delta y = \frac{\alpha}{1 + \alpha}y\)

여기에서 이상적인 $\alpha$ 와 수수료 적용모델에서의 $\alpha_{\rho}$ 에 관계에 주목하면 될 것 같습니다.

\[\Delta y_{\rho} = \frac{\alpha_{\rho}}{1 + \alpha_{\rho}}y\\ \alpha_{\rho} = \gamma \cdot \alpha\\ \Delta y_{\rho} = \frac{\gamma \cdot \alpha}{1 + \gamma \cdot \alpha}y\]

교환이 끝난 최종 상태 \({x^{\prime}}_{\rho} \times {y^{\prime}}_{\rho}\) 와 처음 상태 \(x \times y\) 간에는 \({x^{\prime}}_{\rho} \times {y^{\prime}}_{\rho} > x \times y\) 부등식이 설립하는데, 그 이유는 수수료 만큼 토큰 풀에 유동성이 공급되었기 때문입니다. 실제 스와핑이 계속 발생하면서 $k$ 상수 값이 유동성 공급 모델과 같이 점점 커지게 됩니다.

Cyclic 논문의 배경지식 섹션에서도 수수료가 적용된 CPMM 모델을 사용하고 있으며 기호를 정의하면 다음과 같다.

• ${\delta}_{a}$ : 교환시 공급하는 토큰 A의 양, 앞의 식에서 $\Delta x$ 와 동일한 의미
• ${\delta}_{b}$ : 교환시 수령하는 토큰 B의 양, 앞의 식에서 $\Delta y$ 와 동일한 의미
• ${\gamma}_{a}$ : 교환시 1에서 A토큰에 붙는 수수료 뺀 값, 앞의 식에서 $\gamma$ 와 동일한 의미
• ${\gamma}_{b}$ : 교환시 1에서 B토큰에 붙는 수수료 뺀 값, 앞의 식에서 $\gamma$ 와 동일한 의미

\[{a^{\prime}}_{\rho} \times {b^{\prime}}_{\rho} = (a + {\delta}_{a}) \times (b - \frac{ {\gamma}_{a} \cdot {\gamma}_{b} \cdot b \cdot {\delta}_{a} }{ a + {\gamma}_{a} \cdot {\delta}_{a} })\]

Arbitrage in Cryptocurrency Markets

논문의 해당 절에서는 가상화폐 시장에서 시세차익을 유발하는 거래에 대한 기존 연구를 정리하고 있는데, 이 부분에 대해서는 주제별 관련 논문을 나열함으로써 간략하게 정리하고자 합니다.

TODO

Cyclic Arbitrage Model

이 섹션에서는 순환 시세차익이 가능한 경우를 판별하는 수식을 유도하고 있습니다. 간단하게 생각하면 3개의 토큰 \({A}_{1} \Leftrightarrow {A}_{2} \Leftrightarrow {A}_{3} \Leftrightarrow {A}_{1}\) 구조일 경우 아래와 같은 수식을 본 논문에서는 도출하고 있습니다.

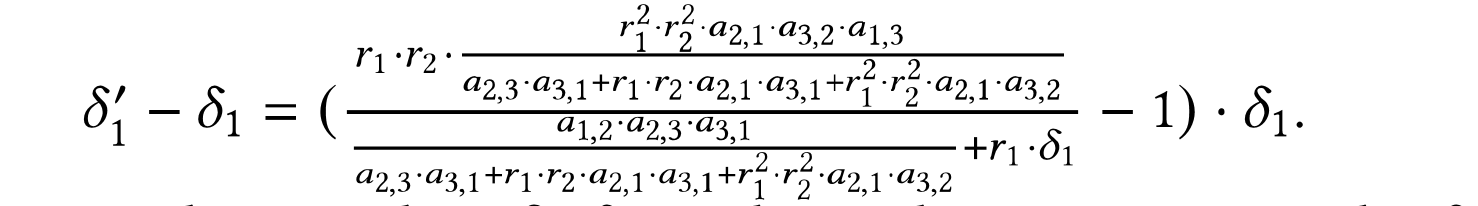수식.1 유효한 순환 시세차익 거래 판별식

한 거래소에서 순환 토큰 거래를 유발한다면, 거래소별 위와 같은 판별식을 도출하는 것은 가능할 것으로 판단됩니다.

Cyclic Arbitrage Opportunities

이 절에서는 순환 매매를 통한 시세차익 거래 기회가 존재하는지에 대한 실제 데이터 분석 결과를 설명하고 있습니다.

Data Collection

시세차인 거래 기회분석을 위해 이더리움 Uniswap-V2관련 데이터를 수집했으며, V2가 실제로 배포된 시점 2020년 5월 4일 10000835블록부터 해서 2021년 4월 15일 12244144블록까지 Uniswap 거래소에서 발생한 트랜젝션을 본 논문의 연구자들이 수집하였습니다.

Profitable opportunities

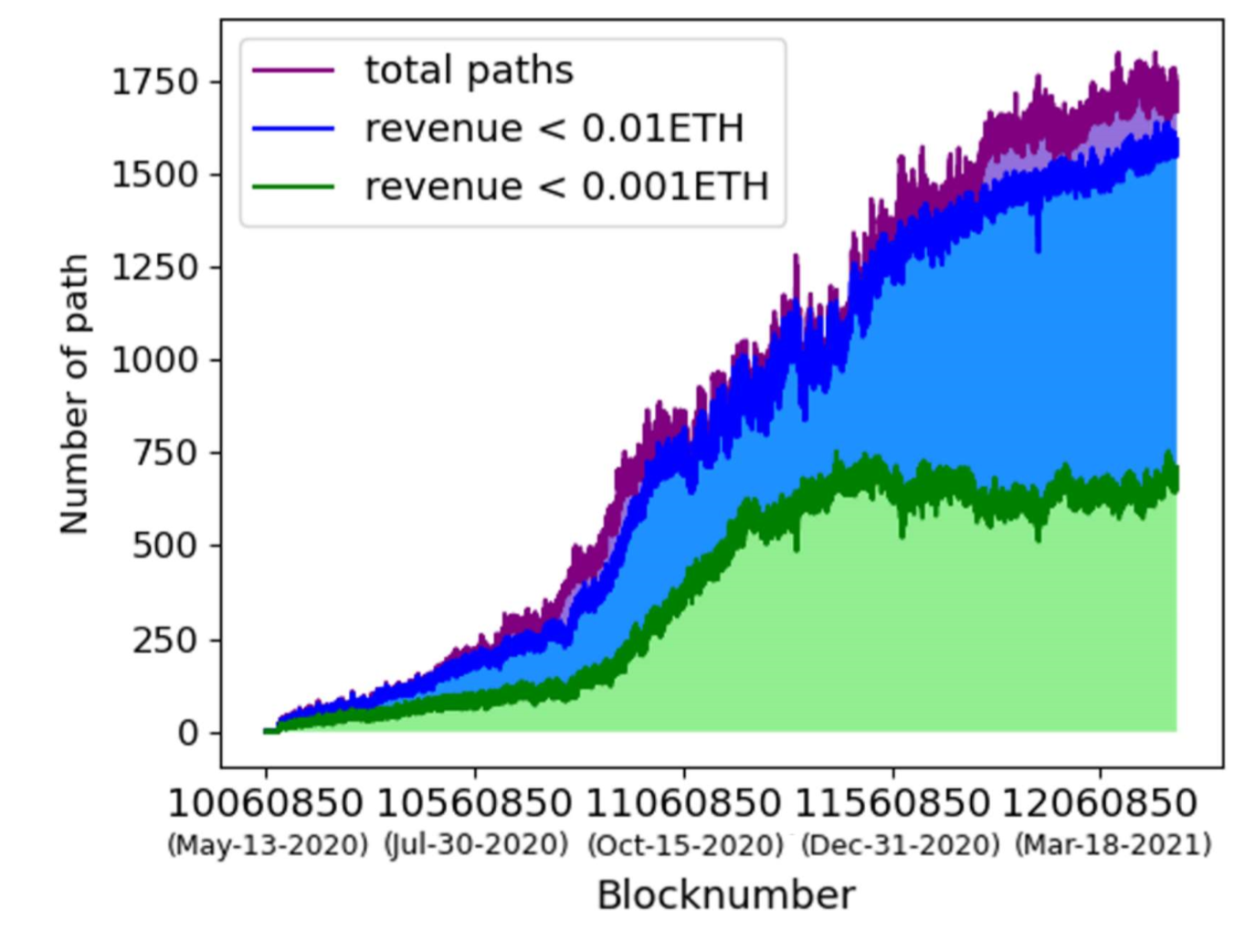
그림 2.를 보면 수익(Revenue) 만들 수 있는 길이3(ETH부터 시작, ETH-A-B-ETH구조) 토큰 패스의 개수를 시간 축으로 표현한 그래프입니다. 해당 그래프를 통해 확인할 수 있는 사실은 마이너에게 지급해야 하는 가스비 0.0001ETH 이상되는 길이3 토큰 패스는 존재한다.는 것과, 논문에서 설명을 하고 있지는 않지만, 상승장으로 진입시 이윤을 만들어 낼 수 있는 경로의 개수가 증가한다는 것입니다. 상승장으로 집입시 DeFi 시장 규모 자체가 커짐으로 좀 더 많은 기회가 생기는 것으로 추정할 수 있습니다.

그림.2 x축은 시간(날짜), y축은 해당 수익(녹색은 0.001ETH 이하, 파란색 0.0001ETH 이상)낼 수 있는 길이3짜리 토큰 패스

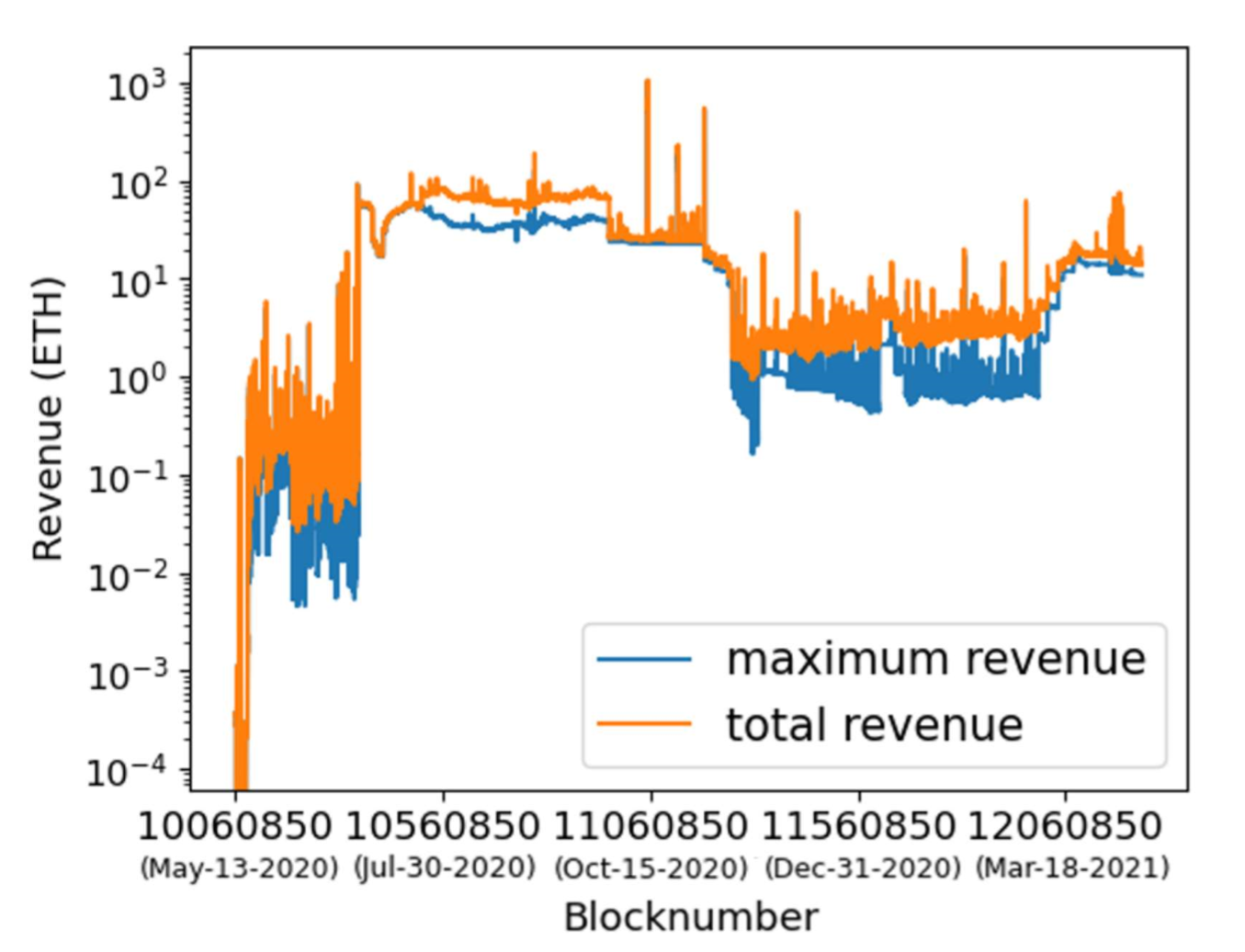
그림 3.은 시간별 순환 시세차익 거래가 만들어 낼 수 있는 수익의 변화와 단일 거래도 만들 수 있는 최대 수익에 대한 그래프입니다. 규모적인 측면에서 당일 거래도 호황기일 때 100ETH 약 지금 ETH 시세로 4억 정도 만들어 낼 수 있음을 볼 수 있습니다. 그림 3에서 2020년 12월부터 본격적인 호황기 진입인데, 전체적인 순환 시세차익 수익이 떨어진 이유와 21년5월이후 수익이 증가한 이유에 대한 해석이 있었으면 했는데 이 두 시점에 대한 해석은 논문에 언급이 없으므로, 추가적인 조사가 필요해 보입니다.

그림.3 x축은 시간(날짜), y축은 해당 수익규모인데 오렌지색은 각각의 순환 시세차익 거래의 수익의 합, 파란색은 단일 순환 시세차익 거래로 만들수 있는 최대 수익

논문에서는 CEX 거래소를 활용한 시세차익 거래 대비 DEX 거래소를 활용한 시세차익 거래의 장점을 아래의 두가지로 설명하고 있습니다.

• Wider range of arbitage : 취급하는 토큰의 개수가 CEX 거래소 대비 매우 많다는 것입니다. 보통 Uniswap과 같은 DEX 거래소 대비 CEX 거래소의 경우 토큰 상장 과정이 까다롭기 때문에 당연히 CEX 거래소에 상장된 토큰 개수가 적습니다. 따라서 시세차익을 만들어 낼 수 토큰 경로가 DEX가 CEX보다 더 많을 수 있고, 논문에 따르면 Uniswap에서 거래될 수 있는 토큰 조합이 30,000개 세계최대 거래소 Binance에서는 토큰 거래 종류가 400개로 거의 100배 정도 차이가 납니다. 반대로 안정성에 대해서 의문을 제기할 수 도 있을 것 같은데 개인적인 견해로는 DEX 순환 시세차익 거래의 시작과 끝 토큰을 CEX 거래소에 상장된 토큰(주로 메인넷 토큰)으로 하면 안정성에 대한 문제도 해결 가능할 것으로 판단됨
• Larger market size : 논문에서는 Makarov와 Schoar의 논문 Trading and arbitarge in cryptocurrency markets을 근거로 이 부분은 설명하고 이는데, 34개의 CEX 거래소에서 발생하는 시세차익 수익이 4개월 동안 20억 USD인 것에 반해서, Uniswap한 곳에서만 하루에 2천4백만 USD의 시세차익이 존재한다고 합니다. 하루에 2천4백만 USD이면 저 중에 정말 작은 부분만이라도 확실하게 먹을 수 있다면, 우리 모두 좋아하는 일만 하면서 살수 있는 삶의 자유(Freedom)를 달성 가능합니다.

Cyclic Arbitrage Markets

논문에서는 Arbitrage Markets으로 제목을 정하고 있는데, 개인적으로는 Cyclic Arbitrage Markets으로 제목을 정하는게 맞을 것 같아서 Cyclic Arbitrage Market으로 변경했습니다. 그 이유는 실제 해당 절에서 저자들이 언급하기를 본인들이 수집하고 분석한 것이 얼마나 많은 “cyclic arbitrages trading”이 실제 시장에서 발생하고 있는지 그리고 얼마나 많은 수익이 생겨나고 있는지를 조사한 내용에 대한 것을 기술하기 때문입니다.

Data Collection

Cyclic arbitrage 거래를 식별하기 위해 휴리스틱으로 접근했다라고 표현하고 있는데, 결국 이 부분은 사람이 많은 부분 판단했다라는 것이며, 기본적으로 100블록 이내(약 25분)안에 이뤄지는 모든 거래 정보를 수집하여 $A \Leftrightarrow B$, $B \Leftrightarrow C$, $C \Leftrightarrow A$ 순서로 스왑핑(swapping) 거래 패턴에 해당하는 거래들을 Cyclic arbitrage 거래로 정의한 것으로 판단됩니다. 여기서 100블록이내의 수행된 트렌젝션으로 제한한 이유는 실제 주관적인 판단이며, 논문 저자들이 DEX내에서 변동성이 큼으로 시세차익 기회를 발견하고, 토큰 사이의 거래가 25분이 넘어가는 것들은 cyclic arbitrage 거래와 관련 없는 거래일 가능성이 높다고 판단했기 때문입니다. 이 부분(25분)은 분석자의 관점에 따라 충분이 변경될 수 있는 부분입니다.

Overall statistics

• 292,606개의 Cyclic arbitrage거래 트랜젝션을 찾음, 그중 287,241개는 ETH로 시작함
• 17,189개의 서로 다른 순환 구조가 존재함, 그중에서 ETH-LCX-REVV 구조가 4710번으로 가장 인기가 많은 순환 구조임
• 265개의 순환 구조만 10번 이상 사용됨
• 전체 순환 시세차익 구조중에서 길이가 3인 경우가 약 85%(247,297)를 차지함

Transacation Number

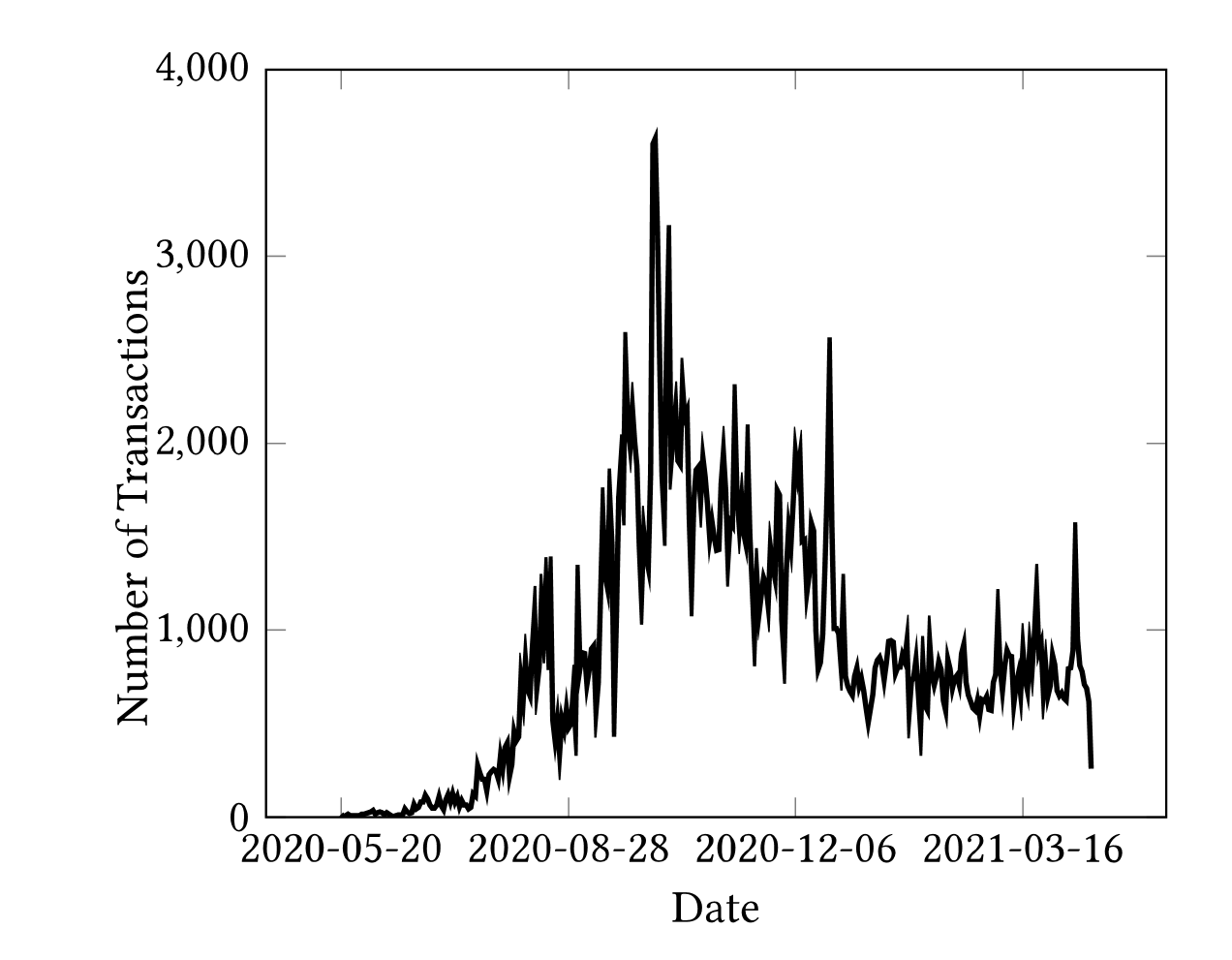
시장의 급하게 커지거나 비트코인의 가격 변동성이 커지면 트렌젝션 수도 급하게 증가하고, 가격이 어느 정도 안정권에 들어가면 일정 수준으로 계속 거래가 이뤄짐을 알 수 있습니다.

그림.4 날짜별 순환 시세차익 매매 트렌젝션 개수

Transacation revenue

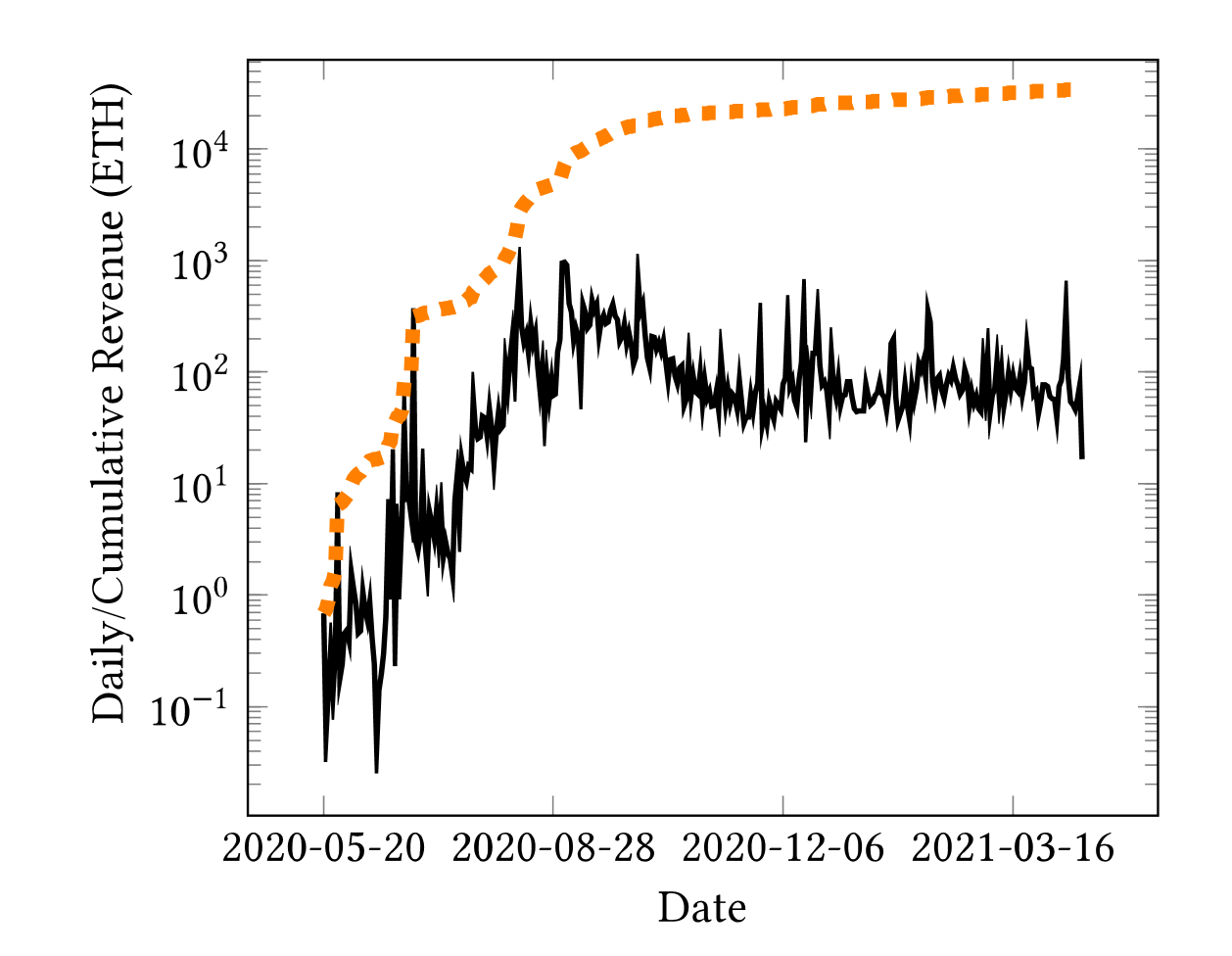
순환 시세차익 거래로 인한 수익 또한 시장에 규모에 비례하는데, 20년 2분기 하루에 약 10ETH정도인 순환 매매의 이익이 21년에는 1000ETH 이상 증가하는 것을 확인할 수 있습니다. 논문에서도 특별한 설명이 없습니다.

그림.5 날짜별 순환 시세차익 수익(검정색:일일수익, 노란색: 누적수익)

Transaction cost

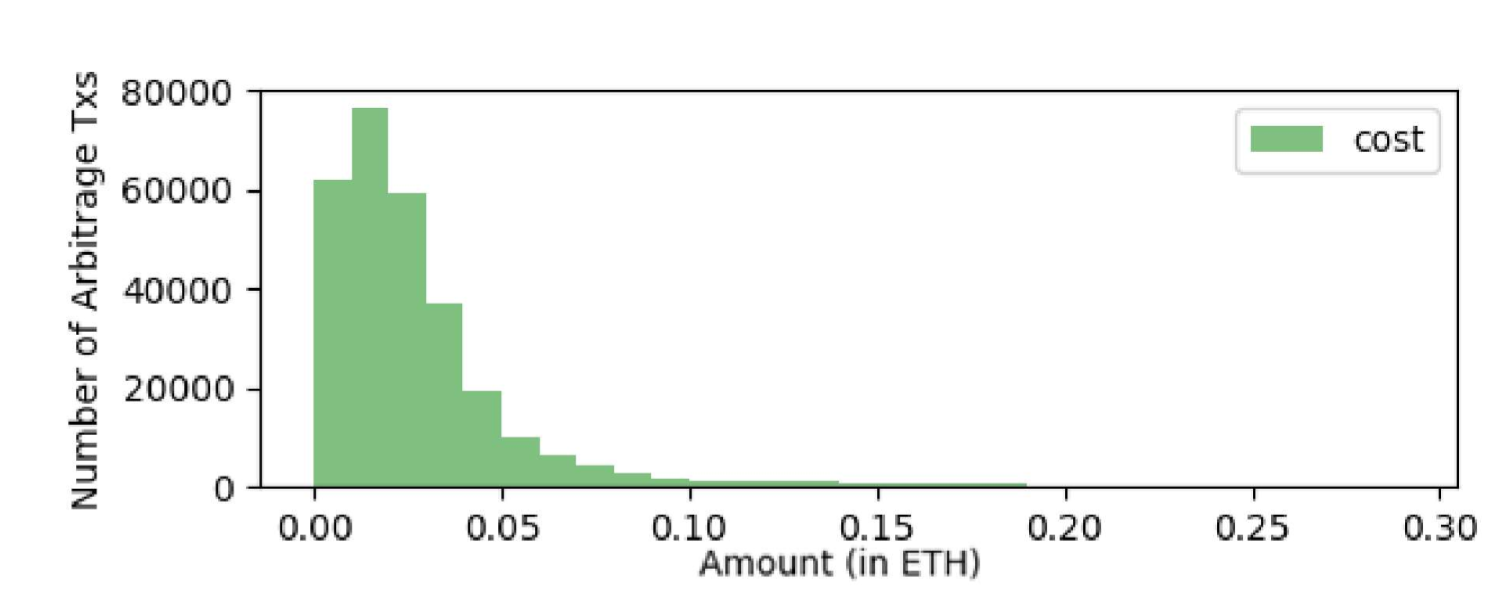
아래 막대 그래프를 보면 전체 트렌젝션의 약 48% 정도가 0.02ETH보다 작은 가스비를 지불하는 것으로 나타났습니다. 전체 수익(34,439.11 ETH)의 약 24.6%(8,458 ETH) 가스비로 지출되는 것도 확인 가능합니다. 요즘 솔라나 네트워크가 많이 느려졌는데, 아마도 솔라나는 트렌젝션 비용이 많이 저렴해서 봇을 마구 돌린다는 얘기가 있습니다. 실제로 본인도 느끼는 것인데 특히 경쟁이 있는 민팅있는 날 더욱더 네트워크가 느려지는 현상이 있습니다.

그림.6 트렌젝션별 가스비의 분포

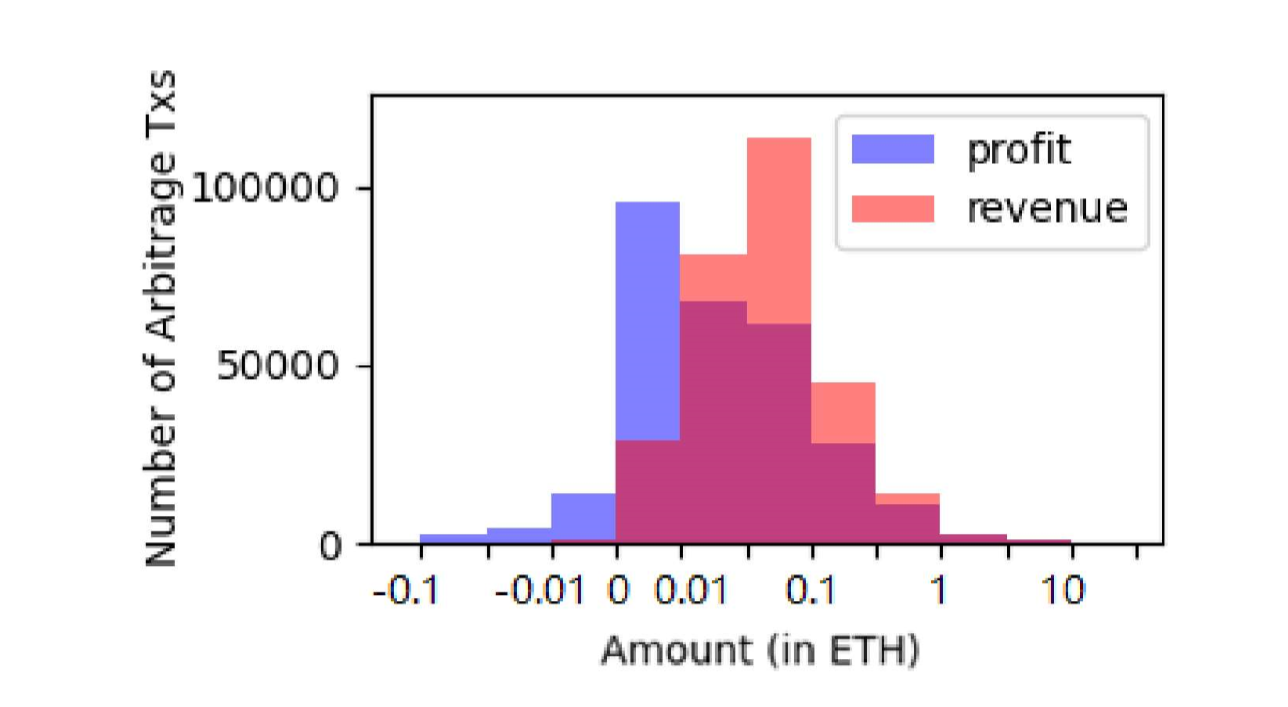
그림 7.에서는 가스비를 고려한 순 이윤에 대해서 설명을 하고 있는데, 개인적으로는 지금도 그림이 직관적으로 이해가 되지 않는데 이부분은 세미나에서 다루고 보완하겠습니다. 논문에서는 해당 그래프를 설명하며, 약 7.1% 트렌젝션의 순수익이 마이너스라고 언급하고, 전체 트렌젝션의 78.4%가 순 이익이 0에서 0.1ETH, 가스비가 0.01에서 0.3ETH에 해당한다고 합니다. 파란색 막대와 주황색 막대외 자주색(?) 막대가 무엇을 의미하는지 명확하지 않습니다. 파란색과 주황색이 겹치는 영역을 표시한 것 같은데 수익 막대와 자주색 막대의 차이가 가스비 및 거래 수수료로 인한 손실을 애기 하고 싶은 건지 해당 그래프가 무엇을 중점적으로 설명하고 싶은 건지 잘 모르겠습니다.

그림.7 트렌젝션별 순이익 및 수익의 분포 분포

Arbitrage Implementation

이 번 섹션에서는 앞에서 분석한 순환 시세차익에 대한 분석이후, 실제 어떤 식으로 구현이 되어있는지에 대한 분석에 대한 내용입니다. 논문에서는 실제 순환 시세차익 거래에 활용된 방법을 두가지로 구분하고 있습니다. 첫 번째는 Sequential implementation방법이고 두 번째는 atomic implementation방법입니다. 기존에 CEX기반의 시세차익 방법에서는 Sequential implmentation방법 밖에 존재할 수 없지만, 블록체인 스마트 컨트렉트 기술을 활용 덕분에 atomic implementation이라는 새로운 방법이 생겼습니다. Sequential implementation는 CEXs에서 시세차익 거래와 비슷하게 동작하게 되는데, 만약에 시세차익 매매를 n개의 토큰을 대상으로 한다면, n번의 순차적인 매매행위가 필요하고, 이를 순차적으로 실행합니다. 반면에 atomic implementation에서는 순환 시세차익 매매를 수행할 때 한 블록체인내에 이뤄질 때에는 n개의 토큰 거래를 하나의 스마트 컨트렉트를 배포함으로써 수행할 수 있으며, 이 동작은 다른 제3자로 인한 방해를 받지 않고, 한 번에 수행됩니다. 따라서 거래의 안전을 보장받을 수 있으며, 만약 수행시 거래 조건이 맞지 않으면 해당 스마트 컨트렉트는 취소(revoke)됩니다.

해당 논문에서는 트렌젝션 분석을 통해 실제 거래봇들의 구현 방식을 확인하였는데, 약 292,518개의 atomic한 순환매매 트렌젝션을 확인하였고, 오직 88개의 순차매매 방식을 확인하였는데, 이 매매는 다른 블록체인간의 순차적인 매매를 위한 것이였습니다. 결국 동일한 블록체인내에서 발생하는 거의 대부분의 시세차익 토큰 매매의 경우 atomic implementation 방식으로 실제로도 구현되어 있음을 확인할 수 있습니다. 또한 재미있는 사실은 위 88개의 순차 매매방식 가운데 46개는 실제로 마이너스 수익을 낸것으로 확인되었다고 논문은 전하고 있습니다. 반면에 atomic implementation의 경우 0.3%만이 마이너스 수익을 기록했다고 합니다. 상대적으로 atomic implementation 방식이 손해가 적은 이유는 단 하나의 거래라도 조건이 맞지 않으면 전체 거래가 취소됨으로써 마이너에게 지급되는 가스비를 제외하면 실제 거래에서 발생하는 손해는 없기 때문이다. 그러면 atomic implementation 방식의 거래의 성공률은 어떻게 될까? 논문는 성공률 측정을 위해 바운더리를 설정하고 있는데, 그 이유는 실패한 트렌젝션의 경우 토큰 교환(swap) 이벤트에 대한 종보가 기록되지 않기 때문입니다. 그래서 성공률 측정을 위한 하한값 도출을 위한 가정은 한 번이라도 순환 매매를 실시했던 트레이더가 유발한 모든 실패한 트렌젝션은 순환매매 트렌젝션이다.라고 가정하는 하는 것입니다. 상한값을 예측하기위한 방법은 실패한 트렌젝션을 평가하기 위해 재생 알고리즘(Time series analysis of ether cryptocurrency prices 논문)을 사용하는 것입니다. 재생 알고리즘으로 실패한 트렌젝션을 수행했을 때 시장에 아무런 영향을 주지 못했다면 실패한 트렌젝션으로 가정하였습니다.

논문에서는 성공률를 두 종류의 스마트 컨트렉트로 구분하여 설명하고 있습니다. 첫 번째는 Private smart contracts이고 다른 하나는 Public smart contracts입니다. Private smart contract의 경우 비유적으로 간단히 설명하면 브라우저에서 클라이언트에서 수행되는 JavaScript코드의 경우 브라우저 소스코드 보기를 통해 그 내용을 확인가능합니다. 그래서 중요 JavaScript의 경우 코드의 보안성을 높이기 위해 JavaScript 난독화(Obfuscation)를 실시하는데 이와 유사한 방식으로 smart contract의 핵심 내용을 숨긴 smart contract를 private smart contract라고 생각하면 됩니다. 조사 결과 smart contract에 privacy를 높이기 위한 몇 몇 솔류션 및 privacy 개념을 소개 하고 있는 해당 블로그참고하면 좋을 것 같습니다. Smart contract의 보안성 문제에 대한 내용 및 관련 기술을 조사하여 BEARS에서도 세미나를 할 계획입니다. 난독화 기술 뿐만 아니라 난독화를 가독화할 수 있는 방법까지 포함하여 폭넓게 다뤄볼 필요가 있을 것 같습니다.

Private smart contracts

Private smart contracts의 경우 하한 성공률은 총 540,054회중 282,563번을 성공하여 약 52%정도의 성공률을 보였습니다. 아무래도 Private smart contracts 기술을 적용하여 구성한 smart contract의 경우 트레이딩 봇으로 사업을 하는 회사수준에서 유지 보수하고 있을 가능성이 높음으로 상대적으로 Public smart contracts대비 높은 성공률을 보이는 것으로 판단됩니다. 성공률 상한같은 경우는 89.6%으로 이는 전문트레이더 측면에서 봤을 때에는 약 90% 이상의 트레이더들이 거래에 성공하는 것으로 나타났습니다. 그리고 이들의 순수익의 경우 실패한 시도까지 포함했을 때 약 21,360ETH 수익을 거두었습니다.

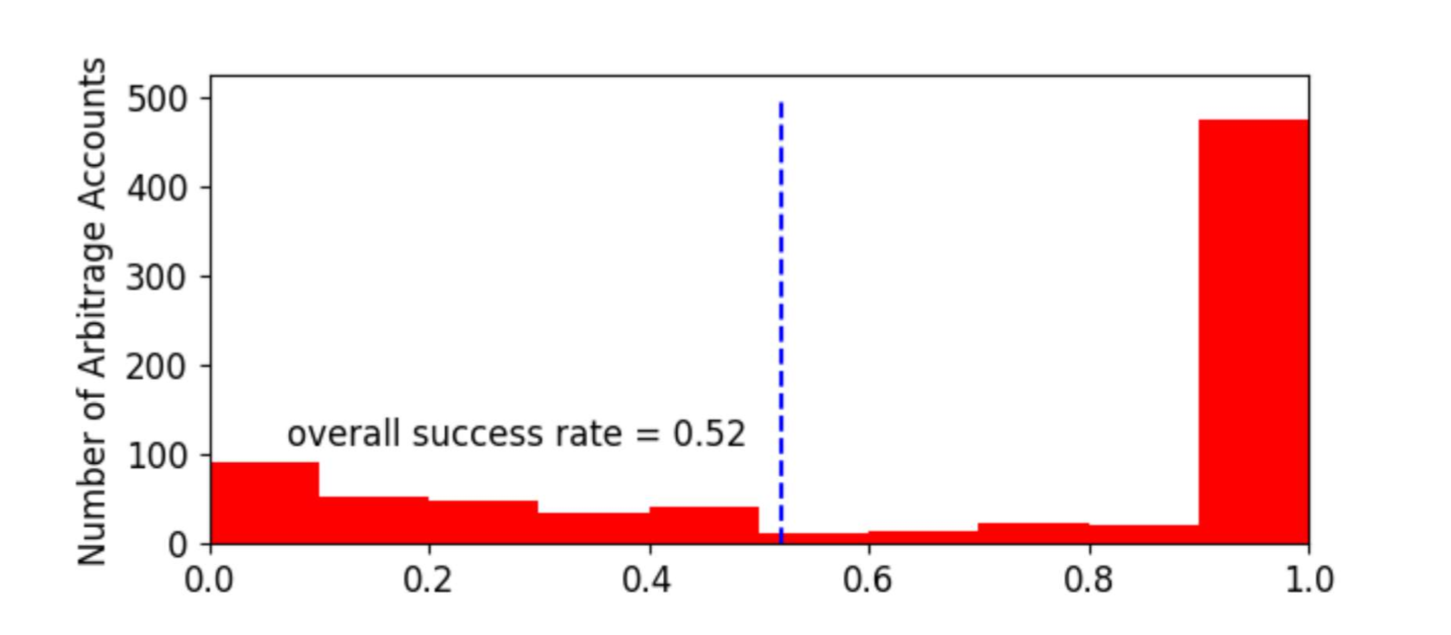그림.8 Atomic Implementation방식의 순환매매의 성공률의 하한

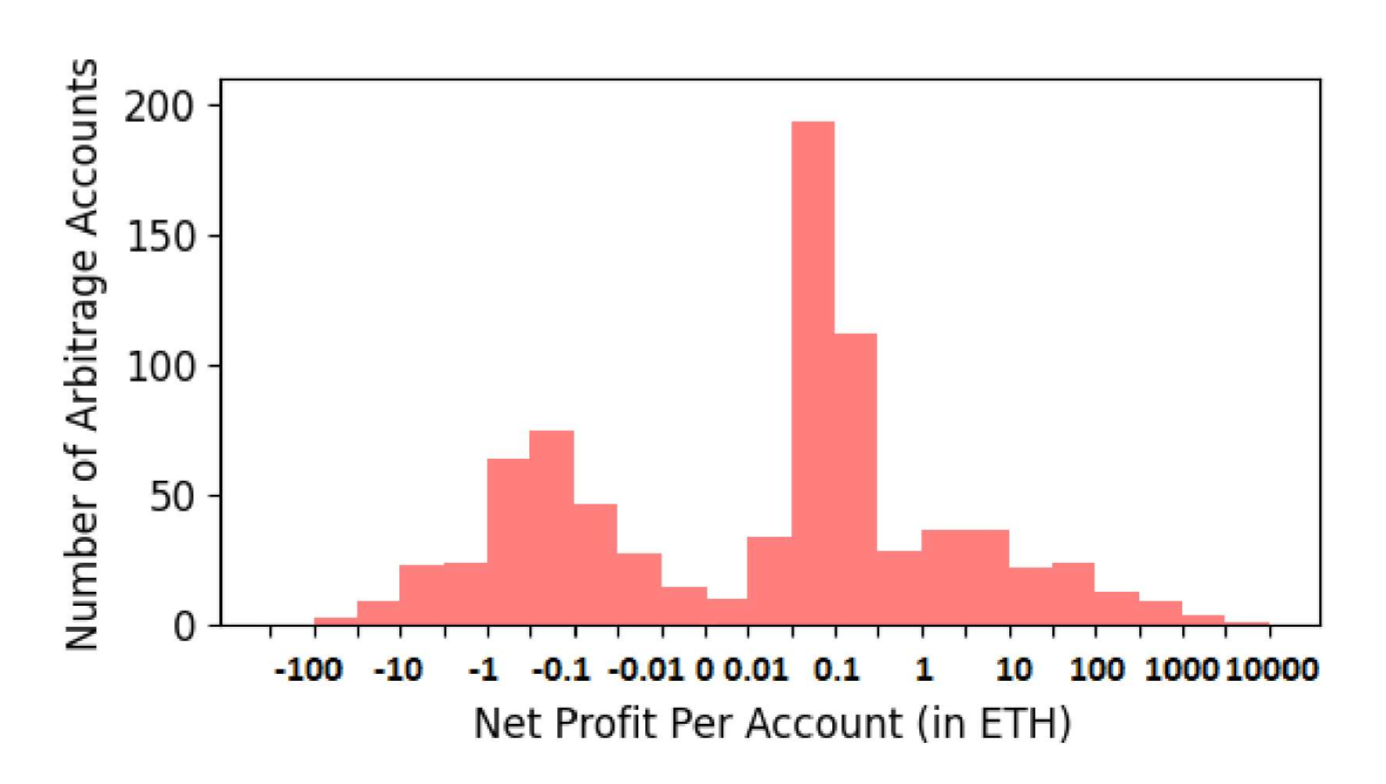그림.9 Atomic Implementation방식의 순환매매의 성공률의 하한일 경우 순수익

Public smart contracts

Public smart contracts의 경우 성공률 하한의 경우 27.3% 이며, 더욱이 실패시 지출한 가스비 또한 224ETH로 private smart contract 192ETH 보다 많다고 논문에서는 기술하고 있습니다. 아마도 개인 투자자들이 실험적으로 atomic implementation을 시도하거나 봇 개발 회사에서 상품화전 간단히 테스트하는 smart contract들이 아닐까?라는 생각이 듭니다. 결론적으로 상대적으로 상용화 전문 업체대비 수익 측면에서 낮은 결과가 나오는게 당연할 수 있습니다.

Conclusion

논문의 결론섹션에서는 주로 저자들이 기여부분을 강조하는 내용이 주 내용이기 때문에 확인하지 않아도 될 것 같고 아래와 같은 앞으로 BEARS 팀에서 연구하거나 조사해야할 업무를 기술함으로서 리뷰글을 마치고자 합니다.

Future Research Topics

해당 논문의 한계점을 바탕으로 DEX내 시스템 트레이딩을 위한 연구(조사/분석 포함) 주제를 생각해보면 다음과 같습니다.

• 솔라나, 테라, 폴카닷과 같은 네트워크에서의 시스템 트레이딩 봇들이 시세차익을 만들어 내는 거래 분석 즉 Cyclic 형태의 트랜젝션을 식별하는 방법 확보를 기반으로 각 체인별 특징을 식별하고, 시세차익 발생 조건식을 도출하는 것을 앞으로의 연구주제로 생각해볼 수 있습니다.
• 초기 CPMM 알고리즘이 아닌 실제 보완된 CPMM알고리즘을 비롯하여 다양한 거래소에서 사용되고 있는 AMM 알고리즘에 대한 시세차익 판단 알고리즘 도출이 필요합니다. Uniswap-V3를 비롯하여 실제 각 DEX 거래소에서 사용하는 AMM 알고리즘에 대한 시세차익 유발 조건에 대해서 확인이 필요합니다.
• 한 DEX 거래소내에서의 토큰 스와핑(Swapping)을 통한 시세차익 뿐만 아니라, 같은 메인넷상 동일한 범주의 AMM 알고리즘을 사용하는 DEX간의 시세차익을 활용해서 시세차익을 만들어 내는 방법, 다른 범주의 AMM 알고리즘을 활용하는 DEX간의 시세차익을 만들어내는 방법, 마지막으로 Flashloan과 같은 블록체인 네트워크에서만 존재하는 특별한 기능을 활용하여 시세차익을 만들어내는 방법에 대한 연구가 필요합니다.
• 또한 Private smart contract 기술에 대한 조사 및 분석이 필요하고, 이를 통해 더 좋은 기술 아이디어에 대한 공유가 필요할 것 같습니다. 기존 x64, 안드로이드 바이너리, 소스코드 난독화에 대한 기존 기술의 핵심 아이디어를 smart contract 분야에 빠르게 적용해서 smart contract의 보안성을 높이는 기술 서비스를 개발한다면 DeFi 시장 규모를 생각할 때 상당한 수익 창출이 가능한 기술이라고 생각합니다.

References

• Formal Specification of Constant Product Market Maker Model and Implementation
• An analysis of Uniswap markets
• Cyclic Arbitrage in Decentralized Exchanges
• SoK: Decentralized Exchanges (DEX) with Automated Market Maker (AMM) Protocols
• https://medium.com/iovlabs-innovation-stories/private-smart-contract-execution-7df89e28eb30
• https://outlierventures.io/wp-content/uploads/2019/11/Diffusion-2019-1.pdf